Huffman coding implementation in Rust
Introduction
Huffman coding is a variable length encoding technique used for lossless data compression. It involves the creation of a binary tree data structure in an elegant way. An opinion sometimes heard on Rust discussion groups is that beginners shouldn’t attempt implementing data structures (linked list, tree etc) as entry level exercises because it is tricky; but we will see that fortunately, the Huffman tree can be created very easily and encoding/decoding based on the tree can also be written as simple functions.
The basic idea
The ASCII encoding for English uses seven bits for each character. For example, the alphabet ‘a’ is represented by 01100001, alphabet ‘b’ by 01100010 and so on .. (each one packed into an 8-bit byte).
Imagine that you are finding out the frequency of occurrence of each alphabet in a text document that you are planning to compress. You see that ‘z’ has a considerably lower frequency of occurrence than ‘a’. Now, it is obvious that if you assign a longer bit pattern to those alphabets which occur less frequently and a shorter bit sequence to those occurring more frequently, you should be able to conserve space.
Let’s say you assign the code ‘10’ to alphabet ‘a’, the code ‘11’ to alphabet ‘b’ and the code ‘1011’ to ‘z’. This encoding satisfies the property that the alphabets which occur more frequently have shorter representations. But, there is a problem. If you encode a ‘z’, when you try to decode it, you can decode it either as ‘z’ or as ‘ab’.
Huffman encoding provides an elegant solution to this problem. Using this technique, you can generate variable length codes with the property that that more frequently occurring alphabets are encoded into shorter bit patterns (and vice versa). Also, each bit pattern will yield a unique alphabet - no pattern will act as a prefix of any other pattern; there will be no ambiguity in the decoding process.
The Implementation
Frequency Counting
Let’s first write a function which will count the number of times each alphabet occurs in a string of alphabets. The basic data structure we need for writing this function is a hash table.
use std::collections::HashMap;
fn frequency(s: &str) -> HashMap<char, i32> {
let mut h = HashMap::new();
for ch in s.chars() {
let counter = h.entry(ch).or_insert(0);
*counter += 1;
}
h
}
The line:
h.entry(ch).or_insert(0)
inserts 0 as the value for the key ‘ch’ (if the key is not present) and returns a mutable reference to the value (refer documentation for HashMap and Entry).
Here is the equivalent Python function:
def frequency(str):
freqs = {}
for ch in str:
freqs[ch] = freqs.get(ch, 0) + 1
return freqs
The Rust code doesn’t look much more verbose or noisy compared to the Python code!
The Huffman tree
Once we get the character frequencies, we can build a Huffman tree which will help us generate optimal encodings for each character in our input text.
To make things easy, let us say the input string is “abaabcd”.
The following code fragment will generate the frequency table for this input:
let f = frequency("abaabcd");
println!("{:?}", f);
Here is the output I got:
{'b': 2, 'a': 3, 'c': 1, 'd': 1}
Let’s look at the Huffman tree built using this frequency table:
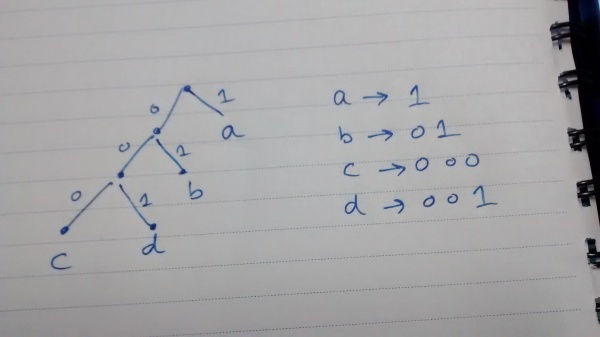
The leaves of the tree are individual alphabets. The edges of the tree are labelled “0” and “1” (left edge is “0”, right is “1”). The “code” for an alphabet is simply the labels on the edges encountered on a traversal of the tree from root node to that particular leaf node.
For example, code for “a” is “1”, you need to traverse only one right edge (labelled “1”) from the root to reach the node containing “a”.
The code for “d” is “001”; you need to move left, left and then right to reach this node from the root.
Note that the alphabet which occurs the most, “a”, has the shortest code “1” and the alphabets which occur the least, “c” and “d”, have 3 bit codes.
If you encode the original message using this scheme, you will use only 13 bits. The same message stored without any encoding in a C character array will consume 56 bits.
Constructing the tree
The logic is simple:
Create a sorted array of tree nodes, where each node will initially contain an alphabet and its frequency.
Take out the two nodes with least frequency values. Create a new tree node and assign the two recently popped nodes as the left and right child nodes of this node. The frequency field of the new node should be equal to the sum of the frequency values in the left and right nodes.
Store the new node in the array and sort the array.
Repeat the above process until the array contains only one element; this will be the root node of the Huffman tree.
Representing the tree node (in C)
If you are coding in C, here is how you would represent the node:
struct node {
int ch;
int freq;
struct node *left, *right;
};
The array will be represented as an array of pointers to dynamically allocated nodes:
struct node *a[N];
How do we represent a tree node in Rust?
Here is a first attempt, leaving out the two pointers:
struct Node {
ch: char,
freq: i32,
}
How do we represent the two left, right pointers? Let’s first see how we can do heap allocation using a Box in Rust.
struct Point {
x: i32,
y: i32,
}
fn main() {
let p = Point {x: 10, y: 20};
}
The definition of “p” in the above program is analogous to the following definition in C:
struct Point p = {10, 20};
The variable “p” is laid out on the stack.
Here is another way to allocate a Point object:
fn main() {
let p = Box::new(Point {x: 10, y: 20});
println!("{:?}", p.x);
}
You can think of this as somewhat similar to the following in C:
struct Point *p = malloc(sizeof(struct Point));
printf("%d", p->x);
A Box in Rust is a pointer to heap-allocated storage.
The following figure shows the same structure allocated on the stack as well as on the heap (using a Box):
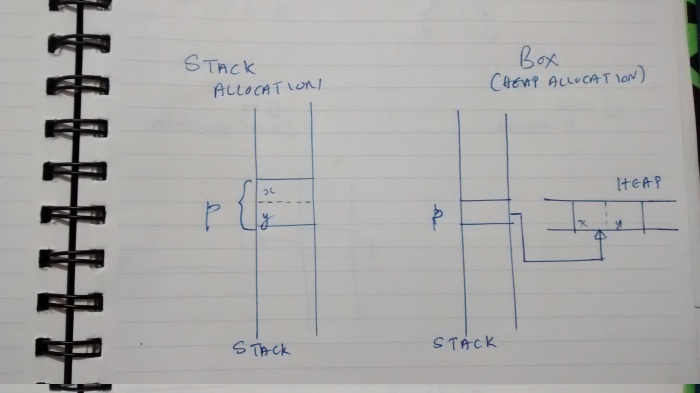
Now, coming back to the tree Node, we can easily represent the two pointers, “left” and “right” as two Boxes:
struct Node {
freq: i32,
ch: char,
left: Box<Node>,
right: Box<Node>,
}
There is another problem. Rust doesn’t have null pointers, so how do you represent the fact that the left or right pointer values may not exist?
Simple, we can use an Option type. The ‘char’ field of non-leaf nodes of the tree also do not contain any valid values, so we can use an Option there also.
Here is the final definition of our tree node type:
struct Node {
freq: i32,
ch: Option<char>,
left: Option<Box<Node>>,
right: Option<Box<Node>>,
}
Just for fun, let’s use this struct to manually build a tree with two nodes - a root node and a child on the left.
fn main() {
let mut p = Box::new(
Node {
freq:10, ch: Some('A'),
left:None, right: None,
});
let q = Box::new(
Node {
freq:4, ch: Some('B'),
left:None, right: None,
});
p.left = Some(q);
println!("{:?}", p);
}
Given a HashMap which maps each alphabet in the input to its corresponding
frequency, it is easy to generate a vector each element of which is a pointer
to a heap allocated Node, ie, Box
fn new_node(freq: i32, ch: Option<char>) -> Node {
Node {
freq: freq, ch: ch,
left: None, right: None,
}
}
fn new_box(n: Node) -> Box<Node> {
Box::new(n)
}
fn main() {
let h = frequency("abaabcd");
let mut p:Vec<Box<Node>> =
h.iter()
.map(|x| new_box(new_node(*(x.1), Some(*(x.0)))))
.collect();
}
You can visualize the iter method turning the hashmap into a sequence of tuples of the form (&k, &v) where each k, v is an element of the hashmap.
The map method takes each (&k, &v) pair and builds a boxed node out of it - the sequence of boxes are then collected together into a vector.
Here is the code which builds the Huffman tree:
while p.len() > 1 {
p.sort_by(|a, b| (&(b.freq)).cmp(&(a.freq)));
let a = p.pop().unwrap();
let b = p.pop().unwrap();
let mut c = new_box(new_node(a.freq + b.freq, None));
c.left = Some(a);
c.right = Some(b);
p.push(c);
}
The sort_by function sorts the vector according to a comparison function passed as a parameter.
The ideal data structure to use here is some kind of a priority queue which provides for fast identification of the max/min element without resorting to sorting. The Rust BinaryHeap is an option. I am using a vector for simplicity.
The pop method returns a Box
When the loop exits, the vector will have just one element in it, and that will be the root of our Huffman tree!
let root = p.pop().unwrap();
Creating the code
After building the tree, we can generate the code for each alphabet by passing the root node of the tree to assign_codes.
let mut h:HashMap<char, String> = HashMap::new();
assign_codes(&root, &mut h, "".to_string());
Here is the definition of assign_codes:
fn assign_codes(p: &Box<Node>,
h: &mut HashMap<char, String>,
s: String ) {
if let Some(ch) = p.ch {
h.insert(ch, s);
} else {
if let Some(ref l) = p.left {
assign_codes(l, h, (s.clone() + "0"));
}
if let Some(ref r) = p.right {
assign_codes(r, h, (s.clone() + "1"));
}
}
}
If the char field of a node is not None, it is a leaf node; so we add that character as the key and s as its code value to the hashmap.
Otherwise, we recursively descend to the left and/or right adding a “0” or a “1” to the current code sequence.
Encoding a message
Given a message, encoding it is simple. Just look up the hashmap for the code corresponding to each character and concatenate all the codes.
fn encode_string(s: &str, h: &HashMap<char, String>) -> String {
let mut r = "".to_string();
let mut t:Option<&String>;
for ch in s.chars() {
t = h.get(&ch);
r.push_str(t.unwrap());
}
r
}
Decoding a message
How do we decode a string of 0’s and 1’s to get the original message? Start from the root of the tree and move left or right depending on whether you get a 0 or 1, stop when you hit a leaf node and emit the character stored in it. Now once again start from the root node and repeat the same process for the remaining part of the encoded string stopping when a leaf node is encountered … repeat till the encoded string is completely consumed.
Here is the implementation of the decoding logic:
fn decode_string(s: &str, root: &Box<Node>) -> String {
let mut retval = "".to_string();
let mut nodeptr = root;
for x in s.chars() {
if x == '0' {
if let Some(ref l) = nodeptr.left {
nodeptr = l;
}
} else {
if let Some(ref r) = nodeptr.right {
nodeptr = r;
}
}
if let Some(ch) = nodeptr.ch {
retval.push(ch);
nodeptr = root;
}
}
retval
}
Conclusion
Here is an excellent tutorial for data structure implementation in Rust. The tree node implementation you see here is based on this document.
Check out my github repo rust-for-fun for the full program.
Check out source code of a Python implementation of Huffman coding by Chris Meyers.